ТЕОРИЯ

4x+8< 64 5x>55

1. Справочный материал

2. Решение неравенств

Определение и основные свойства неравенств.

Определения:

Неравенствами называют выражения вида a<b (a≤ b) ,a>b (a≥b),

где a и b могут быть числами или функциями.

Символы <(≤), >(≥) называются знаками неравенства и читаются соответственно :

меньше(меньше или равно) ,больше(больше или равно).

Неравенства , которые записываются с помощью знаков > и <,называются строгими,

а неравенства, в записи которых участвуют знаки ≥ и ≤,- нестрогими.

Неравенства вида a<x<b (a≤x≤b) называются двойными неравенствами

и читаются соответственно :x больше a,но меньше b (x больше или равно a,но меньше или равно b ).

Различают два вида неравенств: числовые (2>0,7 ;½<6) и неравенства с переменной (5x-40>0 ; x²-2x<0).

Свойства числовых неравенств :

Если a>b , то b<a; если a<b, то b>a.
Если a<b и b<c, то a<c.
Если a<b и c-любое число, то a +c<b+c.
Если a<b и c>0,то ac<bc. Если a<b и c<0,то ac>bc.
Если a<b и c<d,то a +c<b +d.
Если a<b и c<d,где a, b, c, d-положительные числа, то ac<bd.

Числовые промежутки

Неравенство	Числовой промежуток	Название промежутка	Геометрическая интерпретация
		*замкнутый промежуток(отрезок) с концами a и b ,a<b*
		*открытый промежуток (интервал) с концами a и b ,a<b*
		*полуоткрытые промежутки (полуинтервалы) концами a и b ,a<b*
		*бесконечные промежутки (лучи)*
		*бесконечные промежутки (открытые лучи)*
		*бесконечный промежуток (числовая прямая)*

Вверх

Основные определения и свойства.

Определения:

Решением неравенства с одной переменной называется значение переменной,

которое обращает его в верное числовое неравенство.

Решить неравенство — значит найти все его решения или доказать, что решений нет.

Неравенства, имеющие одни и те же решения, называются равносильными.

Неравенства, не имеющие решений, также считают равносильными.

При решении неравенств используются следующие свойства:

1) Если из одной части неравенства перенести в

другую слагаемое с противоположным знаком,

то получится равносильное ему неравенство.

2) Если обе части неравенства умножить или

разделить на одно и то же положительное число,

то получится равносильное ему неравенство.

3) Если обе части неравенства умножить или

разделить на одно и то же отрицательное число,

изменив при этом знак неравенства на противоположный,

то получится равносильное ему неравенство.

Многие неравенства в процессе преобразований сводятся к линейным неравенствам.

Неравенства вида ах>b ( ах <b ,ax≤b или ax≥b), где а и b — некоторые числа,

называют линейными неравенствами с одной переменной.

Если a>0 ,то неравенство ax>b равносильно неравенству

и множество решений неравенства есть промежуток

Если a<0 ,то неравенство ax>b равносильно неравенству

и множество решений неравенства есть промежуток

неравенство примет вид 0∙x>b, т.е. оно не имеет решений ,если b≥0,

и верно при любых x ,если b<0.

Аналитический способ решения неравенств с одной переменной.

Алгоритм решения неравенства с одной переменной

Преобразовать обе части неравенства.
Привести подобные слагаемые.
Привести неравенства к простейшему виду, на основании свойств неравенств.
Записать ответ.

Приведем примеры решения неравенств .

Пример 1. Решить неравенство 3x≤15.

Решение:

Обе части неравенства

разделим на положительное число 3 (свойство 2) : x≤5.

Множество решений неравенства представляет собой числовой промежуток (-∞;5].

Ответ :(-∞;5]

Пример 2. Решить неравенство -10x≥34.

Решение:

Обе части неравенстваразделим на отрицательное число -10 ,

при этом знак неравенства изменим на противоположный (свойство 3) : x≤-3,4.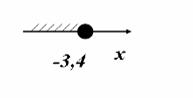

Множество решений неравенства представляет собой промежуток (-∞;-3,4].

Ответ : (-∞;-3,4].

Пример 3. Решить неравенство 18+6x>0.

Решение:

Перенесем слагаемое 18 с противоположным знаком в левую часть неравенства (свойство 1): 6x>-18.

Разделим обе части на 6 (свойство 2) :

x>-3.

Множество решений неравенства представляет собой промежуток (-3;+∞).

Ответ : (-3;+∞).

Пример 4.Решить неравенство 3(x-2)-4(x+2)<2(x-3)-2.

Решение:

Раскроем скобки : 3x-6-4x-8<2x-6-2.

Перенесем члены ,содержащие неизвестное ,в левую часть ,

а члены не содержащие неизвестное , в правую часть (свойство 1):

3x-4x-2x<6+8-6-2.

Приведем подобные члены: -3x<6.

Разделим обе части на -3 (свойство 3) :

x>-2.

Множество решений неравенства представляет собой промежуток (-2;+∞).

Ответ : (-2;+∞).

Пример 5. Решить неравенство

Решение:

Умножим обе части неравенства на наименьший общий знаменатель дробей,

входящих в неравенство, т. е. на 6 (свойство 2).

Получим:

2x-3x≤12.

Отсюда , -x≤12 , x≥-12.

Ответ : [-12;+∞).

Пример 6. Решить неравенство 3(2-x)-2>5-3x.

Решение:

Упростим неравенство ,раскрыв скобки:

6-3x-2>5-3x, 4-3x>5-3x, -3x+3x>5-4.

Приведем подобные члены в левой части неравенства и запишем результат в виде 0∙x>1.

Полученное неравенство не имеет решений, так как при любом значении x

оно обращается в числовое неравенство 0 < 1, не являющееся верным.

Значит, не имеет решений и равносильное ему заданное неравенство.

Ответ : решений нет.

Пример 7.Решить неравенство 2(x+1)+5>3-(1-2x).

Решение:

Упростим неравенство ,раскрыв скобки:

2x+2+5>3-1+2x, 2x+7>2+2x,2x-2x>2-7, 0∙x>-5.

Полученное неравенство является верным при любом значении x,

так как левая часть при любом x равна нулю, а 0>-5.

Множеством решения неравенства является промежуток (-∞;+∞).

Ответ : (-∞;+∞).

Пример 8. При каких значениях x имеет смысл выражение:

Решение:

а)По определению арифметического квадратного корня

должно выполнятся следующее неравенство 5x-3≥0.

Решая, получаем 5x≥3, x≥0,6.

Итак, данное выражение имеет смысл при всех x из промежутка [0,6;+∞).

Ответ : [0,6;+∞).

б)С учетом свойств арифметического квадратного корня и знаменателя дроби

должно выполнятся следующее неравенство 2-3x>0.

Отсюда ,-3x>-2 (свойство 3), x<2/3.

Данное выражение имеет смысл при всех x из промежутка (-∞;2/3).

Ответ :(-∞;2/3).

Пример 9.При каких значениях a квадратное уравнение x-8x²-4a=0 имеет два корня ?

Решение:

Квадратное уравнение будет иметь два корня ,если дискриминант D будет больше нуля.

D=(-8)²-4∙(-4a)=64+16a,

64+16a>0,

16a>-64,

a>-4.

Таким образом , при всех значениях a из промежутка (-∞;-4)

данное квадратное уравнение будет иметь два корня.

Ответ : при всех a из промежутка (-∞;-4) .

Пример 10.Решите задачу:

В одном бассейне налито 100 л воды, а во втором 150 л воды.

Каждый час в первый бассейн вливается 15 л воды, а во второй - 5 л воды.

В какие моменты времени в первом бассейне будет больше воды, чем во втором?

Решение:

Пусть за x ч в первый бассейн вольется 15x л воды и в нем станет 100+15x л воды.

Тогда через x ч во втором бассейне будет 150+5x л воды.

Надо найти такие значения x , для которых выполняется неравенство

100+15x>150+5x.

Преобразовав ,получаем

15x-5x>150-100,

10x>50,

x>5.

Итак ,в первом бассейне окажется больше воды ,чем во втором, при x>5,

т.е. после 5ч с начала вливания воды.

Ответ : после 5ч с начала вливания воды.

Пример 11. При каких значениях x значения функции Y=-1/3x+8 принадлежит промежутку (-1,1)?

Решение: -1<-1/3x+8<1,

-9<-1/3x<7,

27>x>21,

21<x<27.

Ответ : (21;27).

? ? ?

Вопросы.

1. Что называется неравенством первой степени с одним неизвестным?

2. Что называется решением неравенства с одним неизвестным?

3. Что значит решить неравенство с одним неизвестным?

4. Каким способом можно решить неравенство первой степени с одним неизвестным?

.Графический способ решения неравенств с одной переменной.

Покажем, как можно, применяя графический метод, решить неравенства вида

kx+ b> 0 (1)

или

kx + b<0, (2)

где k и b — заданные числа и k≠0.

В декартовой системе координат Оху рассмотрим прямую

y = kx + b. (3)

На рис. 1 изображена такая прямая при k> 0, а на рис. 2 изображена такая прямая при k<0.

рис1. рис.2.

Решить неравенство (1) — это значит найти все решения х,

для которых прямая y = kx-b расположена выше оси х.

Здесь важную роль играет точка А пересечения прямой (3) с осью х.

Абсциссу точки А обозначим через x_o. Так как ее ордината равна нулю, то x_o удовлетворяет уравнению

O = kx_o + b, откуда

x_o=-b/k.

Обратимся к рис. 1, соответствующему случаю k> 0. Мы видим , что прямая y = kx+b

расположена выше оси х для всех х, находящихся правее точки x_o, т. е. для всех х из интервала (-∞, + ∞), и расположена ниже оси х для всех х, находящихся левее точки x_o, т. е. для всех х из интервала (—∞,x_o).

Итак, при k> 0 неравенство (1) выполняется на интервале (x_o, + ∞), а неравенство (2) —на интервале (—∞,x_o).

При k<0, как это видно из рис. 2, неравенство (1) выполняется на интервале (—∞,x_o),

а неравенство (2) — на интервале (x_o, + ∞).

Пример 1. Решить, применяя графический метод, неравенства

2X+1 >0, (4)

2X+1 <0. (5)

Решение :

Начертим в декартовой системе координат Оху прямую

у = 2X+1. (6)

рис3.

Для этого нужно знать две ее точки. В качестве первой точки возьмем точку пересечения прямой с осью х. Она все равно будет нужна. Полагая в формуле (6) у = 0, получим уравнение

0 = 2х+1.

Его решение есть абсцисса точки А пересечения прямой с осью х. Итак, А ( —1/2 ,0).

В качестве второй точки можно взять точку В пересечения прямой с осью у. Ее абсцисса X=0, а ордината

y=2∙0+1, y=1.

Итак, В(0, 1).

Через точки А и В проводим прямую. Это и есть прямая y=2X+1 (рис. 3).

Из рис. 3 видно, что неравенство (4) выполняется на интервале ( — 1/2 , + ∞) а (5) — на интервале (— ∞, —1/2).

? ? ?

Вопрос.

Как можно решать неравенства первой степени, применяя графический метод?